Struktury drzewiaste (ang. Tree Data Structures) są obecne w niemal każdej aplikacji i stronie internetowej, a podstawowa wiedza na ich temat jest niemal niezbędna dla każdego programisty i programistki. Niezależnie od tego, czy zajmujesz się frontendem, backendem, czy aplikacjami mobilnymi, prędzej czy później natrafisz na dane, które będą prezentowane w formie drzewa.

W artykule skupiam się na podstawowych zagadnieniach, które są niezbędne do zrozumienia drzew, ich budowy i zastosowania. Po przeczytaniu będziesz mieć solidne podstawy oraz punkt startowy do rozpoczęcia swojej przygody ze światem struktur danych.

Żeby zrozumieć drzewa trzeba zacząć od grafów. Z pewnością zetknąłeś lub zetknęłaś się już z tym terminem i być może to słowo przywołuje u Ciebie wspomnienia z lekcji matematyki. Okazuje się, że w programowaniu wykorzystujemy dokładnie tą samą strukturę.

Zacznijmy zatem od krótkiego przypomnienia podstawowych terminów i wyjaśnienia czym właściwie jest graf. Graf to struktura złożona z wierzchołków (ang. vertices) oraz krawędzi (ang. edges), które te wierzchołki ze sobą łączą. W potocznej mowie spotkasz się także z określeniem “węzeł” (ang. node), które jest synonimem wierzchołka. W tym artykule również używam tych dwóch pojęć wymiennie.

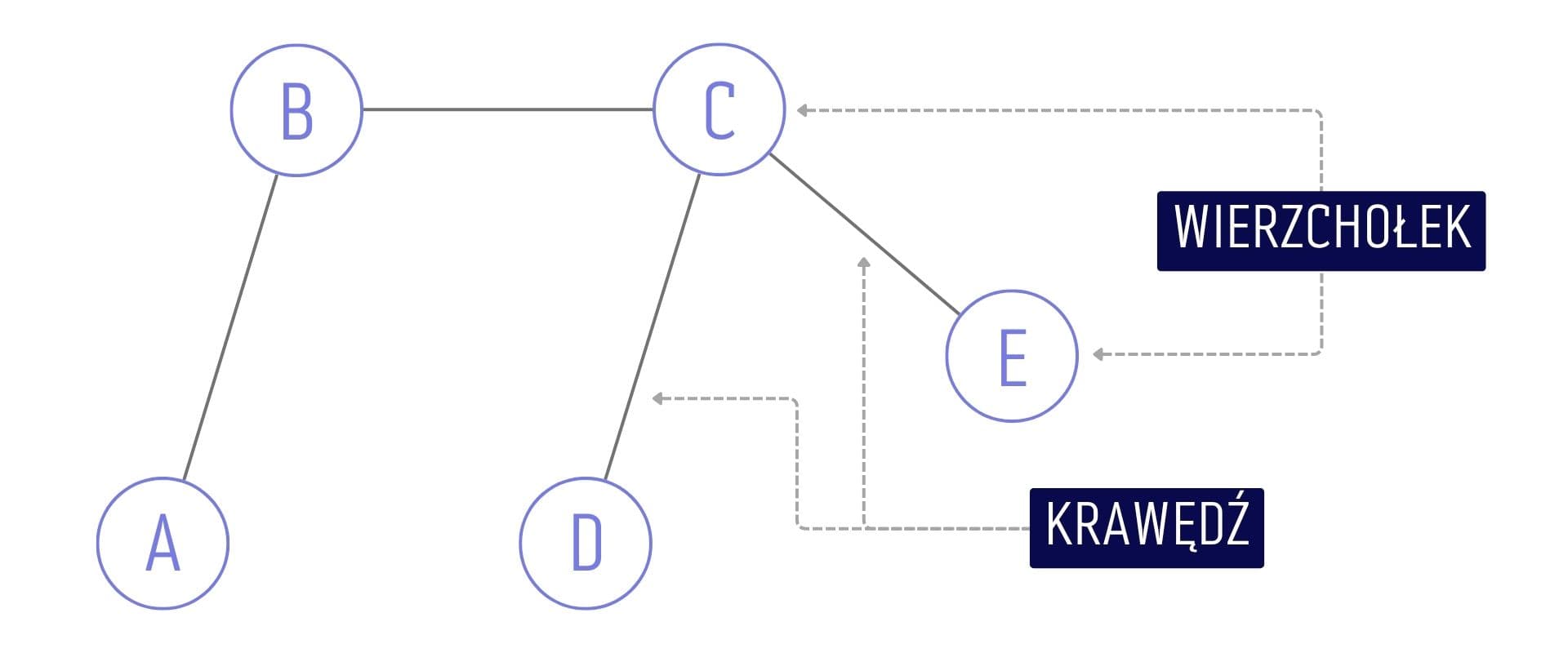
Acykliczny, nieskierowany oraz nieważony graf

Przedstawiony powyżej graf jest acykliczny, nieważony i nieskierowany jednocześnie. Za tymi trzema terminami kryją się dość proste do wyjaśnienia zasady:

• Acykliczność: oznacza, że graf nie posiada ani jednego cyklu. Cykl to kilka połączonych ze sobą wierzchołków, które tworzą zamkniętą drogę, a jej ostatnia krawędź kończy się w wierzchołku w którym ta droga się zaczęła. Jeżeli nadal brzmi to enigmatycznie, to z pewnością zrozumiesz zasadę działania cyklu po przedstawieniu tego na rysunku.

• Waga: każda krawędź grafu może mieć przypisaną wagę. Jeżeli do żadnej z krawędzi grafu nie jest przypisana waga, to taki graf nazywamy nieważonym. Wagi można porównać do czasu przejazdu pomiędzy miastami, krawędzie do dróg, a wierzchołki do miast. Przypuśćmy, że wybierasz się z Warszawy do Łodzi. Czas przejazdu wyniesie 90 minut, a więc waga krawędzi to 90.

• Kierunek: krawędzie mogą wskazywać na kierunek połączenia wierzchołków. W przypadku grafu przedstawionego powyżej tego nie robią. Oznacza to, że węzeł A jest połączony z węzłem B, ale też wierzchołek B jest połączony z wierzchołkiem A. Można o nich myśleć, jak o ulicach dwukierunkowych. W przypadku określenia kierunku krawędzi, mamy do czynienia z ulicami jednokierunkowymi.

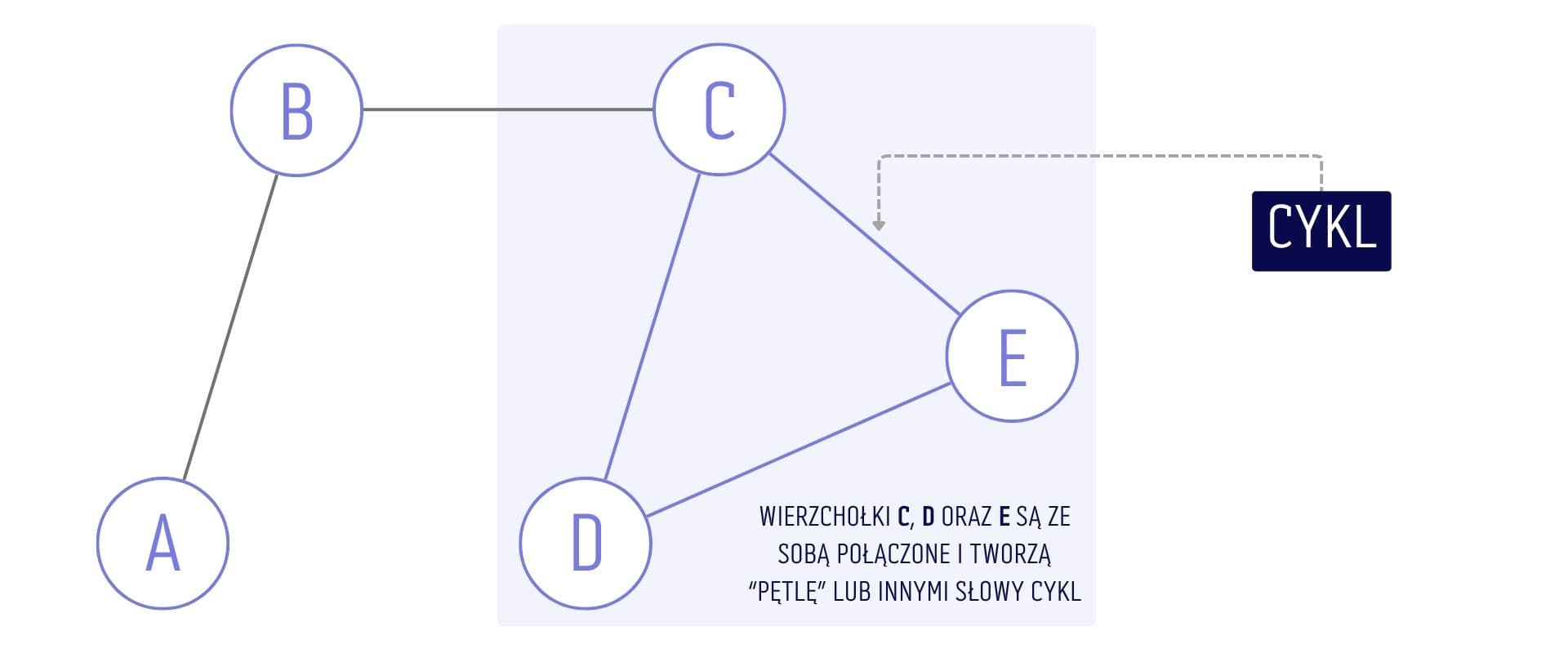
Nieskierowany graf, zawierający jeden cykl

Nie bez powodu porównywałem poszczególne elementy grafu do realnego świata, gdzie wierzchołki to miasta, krawędzie to ulice, a ich wagi to czas przejazdu z punktu A do punktu B. Zrobiłem to, ponieważ grafy są bardzo często stosowane w systemach nawigacji. Jeżeli zdarzyło Ci się korzystać np. z Google Maps, to nieświadomie korzystałeś/aś również z grafów.

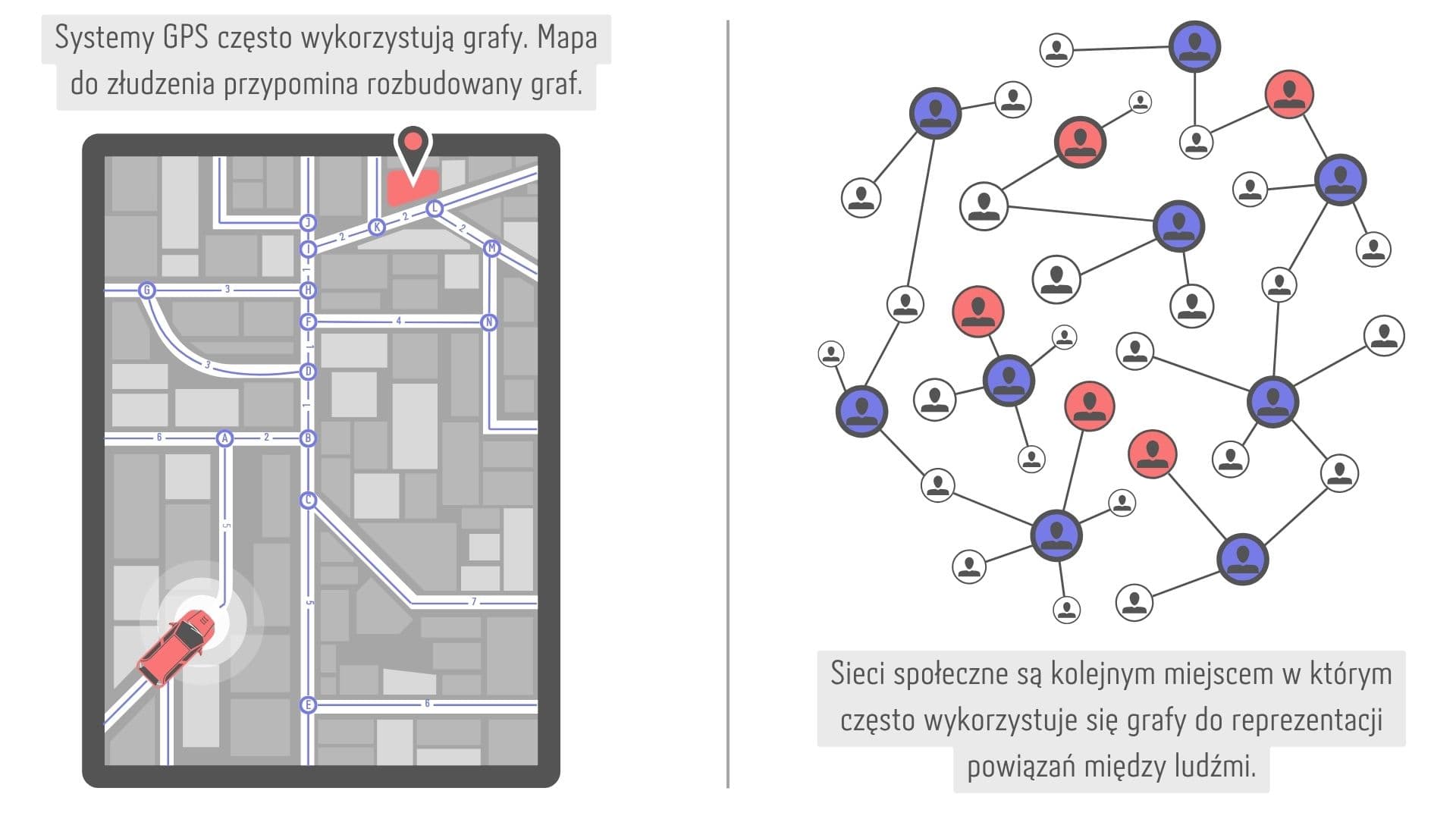
Graf wykorzystany w nawigacji oraz sieciach społecznych

Mapy nie są jedynym miejsce gdzie możemy znaleźć grafy. Gdybyśmy chcieli ująć temat znacznie bardziej ogólnie, to można by powiedzieć, że grafy są używane wszędzie tam, gdzie trzeba w jakiś sposób reprezentować powiązania pomiędzy poszczególnymi elementami. Mogą to być sieci społeczne (np. Facebook), systemy rekomendacji, sztuczna inteligencja, a nawet sam internet, którego fizyczne elementy (routery, switche, itp.) tworzą ogromny graf.

JavaScript nie posiada wbudowanych w język typów służących do reprezentacji grafu. To jednak nie problem, ponieważ możemy wykorzystać obiekt do reprezentacji zarówno wierzchołka jak i krawędzi (jeżeli mamy do czynienia z krawędziami ważonymi).

Oczywiście grafy to znacznie bardziej rozbudowany temat, jednak moim celem nie jest dogłębne wyjaśnienie wszystkich możliwych terminów (co byłoby niezwykle trudne w jednym artykule), a jedynie wprowadzenie do tego świata. Ta wiedza jest również niezbędne do zrozumienia drzew, czyli głównego tematu artykułu.

Naukę o drzewach rozpoczęliśmy od grafów nie bez przyczyny. Okazuje się, że struktury drzewiaste to tak naprawdę rodzaj grafu. Jednak w przeciwieństwie do grafu, drzewo ma jeden wierzchołek główny, nazywany korzeniem (ang. root). Oznacza to, że na najwyższym poziomie drzewa może istnieć tylko jeden węzeł. 

Istnieją jeszcze dwie zasady, które dotyczą wszystkich drzew: brak cykli oraz maksymalnie jeden rodzic dla poszczególnego węzła. Można zatem powiedzieć, że drzewo to rodzaj grafu acyklicznego (skierowanego lub nieskierowanego), którego wszystkie węzły, z wyjątkiem węzła głównego, posiadają tylko jednego rodzica. Warto w tym miejscu zaznaczy, że poszczególne rodzaje drzew mają znacznie więcej ograniczeń i wymogów, a te które poznaliśmy do tej pory dotyczą wszystkich struktur drzewiastych.

Za chwilę przejdziemy do praktyki ale zanim to zrobimy, musimy jeszcze poznać kilka podstawowych terminów związanych z drzewami:

• Korzeń (ang. root) - to węzeł główny, znajdujący się na szczycie drzewa. Od niego wychodzą wszystkie pozostałe węzły drzewa. W przeciwieństwie do pozostałych węzłów, korzeń nie posiada węzła-rodzica.

• Rodzic (ang. parent) - węzeł nadrzędny (znajdujący się powyżej) danego węzła. W przykładzie poniżej, rodzicem węzła C jest węzeł A. Wszystkie węzły w drzewie, z wyjątkiem korzenia, posiadają jednego rodzica.

• Dziecko (ang. child) - węzeł potomny (znajdujący się poniżej) danego węzła. W poniższym przykładzie, węzeł A jest rodzicem węzła C, co oznacza, że węzeł C jest dzieckiem węzła A.

• Liść (ang. leaf) - węzeł końcowy, który nie posiada dzieci. Liściem jest każdy węzeł, który nie posiada węzłów potomnych. W naszym przykładzie są to węzły E, D oraz B.

• Poddrzewo (ang. subtree) - to wybrana część drzewa, która nie rozpoczyna się w węźle głównym. W poniższym przykładzie, poddrzewem mogą być węzły C, D, E oraz B. Węzeł C jest korzeniem tego poddrzewa, a węzły D i E jego dziećmi. Poddrzewo rozpoczynające się w węźle B, zawiera tylko korzeń.

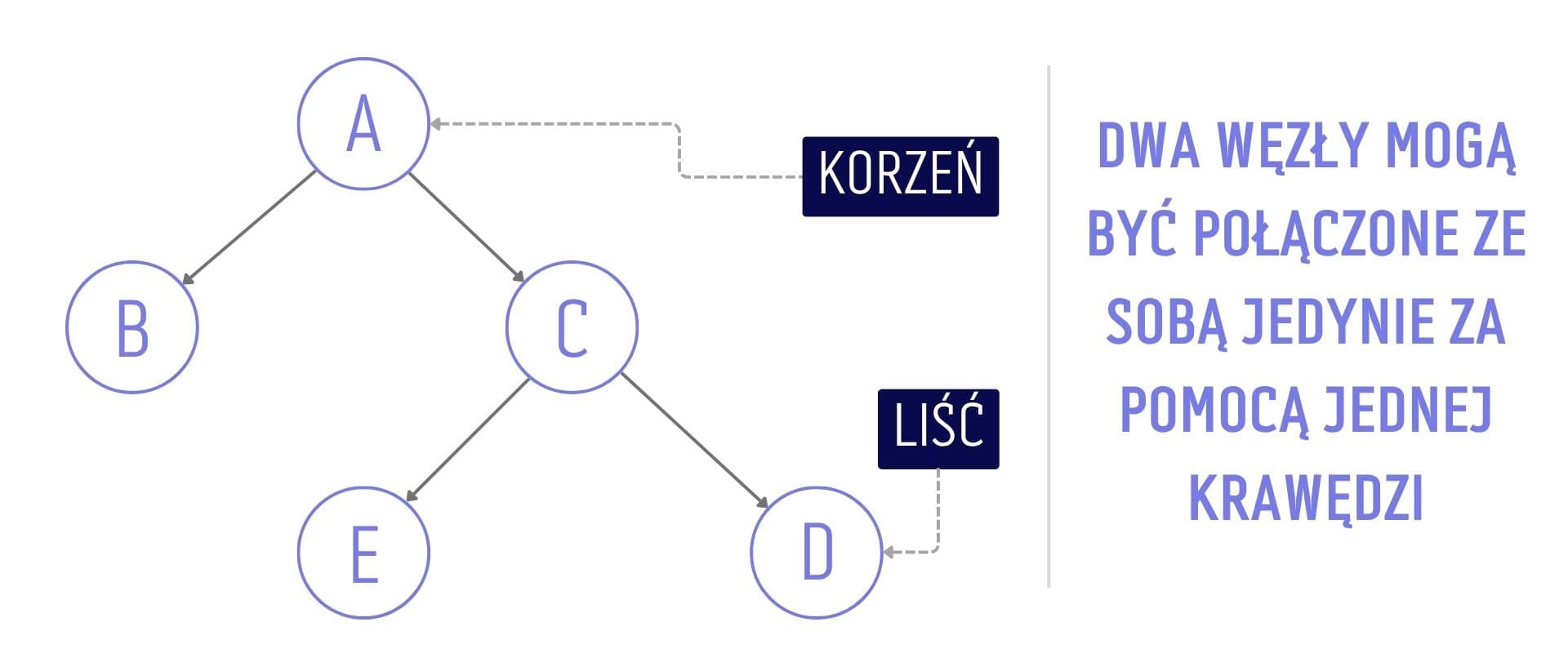
Graficzna reprezentacja drzewa

Pozostało nam odpowiedzieć na jeszcze jedno pytanie: jak przedstawić takie drzewo w JavaScript?

Podobnie, jak w przypadku grafów, możemy to zrobić wykorzystując obiekty i klasy. Jednak tym razem, musimy pamiętać o ograniczeniach związanych ze strukturą drzewa: każdy węzeł może mieć tylko jednego rodzica, a drzewo może posiadać tylko jeden korzeń. Nie może być w nim również cykli.

Klasa, którą się posłużyliśmy to jedna z najprostszych implementacji. Z jej pomocą możemy tworzyć poszczególne węzły drzewa, a następnie połączyć je w całość. Minus takiego podejścia polega na tym, że całe drzewo musimy utworzyć manualnie, co nie jest zbyt praktyczne. W związku z tym, taki kod spotkasz najczęściej w zadaniach rekrutacyjnych i teoretycznych rozważaniach. Dodatkowo wszelkie modyfikacje będą wymagały ręcznego wyszukiwania i zmieniania węzłów. 

Z tych właśnie powodów, zazwyczaj spotkasz się ze znacznie bardziej rozbudowaną wersją niż ta, którą Ci pokazałem, choć nierzadko będzie ona schowana za zgrabną warstwą abstrakcji i udstępni na zewnątrz jedynie niewielki interface. Warto jednak zwrócić uwagę, że sama implementacja może różnić się w zależności od rodzaju drzewa i jego przeznaczenia, a tych jest bardzo dużo.

W świecie programowania, podobnie jak w przyrodzie, istnieje wiele różnych rodzai drzew. Każde z nich ma swoje plusy i minusy, a co za tym idzie, znajduje zastosowanie w innych przypadkach. Opisanie wszystkich możliwych typów struktur drzewiastych wymagałoby napisania książki dlatego w tym artykule skupimy się na tych, które są najczęściej stosowane.

Linked List - To jedna z najpopularniejszych struktur. Jak sama nazwa wskazuje, jest to lista połączonych ze sobą węzłów z których każdy posiada tylko jedno dziecko. Technicznie jest to również drzewo, ale jej popularność sprawiła, że doczekała się swojej własnej nazwy.

Lista połączona jest niezwykle przydatna w przypadku, gdy nie możemy lub nie chcemy wykorzystać tablicy. Sprawdza się szczególnie dobrze wtedy, gdy chcemy dodawać do niej wiele nowych elementów, ponieważ nie wymaga rezerwowania ciągłego bloku pamięci, a w przypadku dodawania kolejnych wartości nie muszą występować one po kolei w fizycznej pamięci komputera.

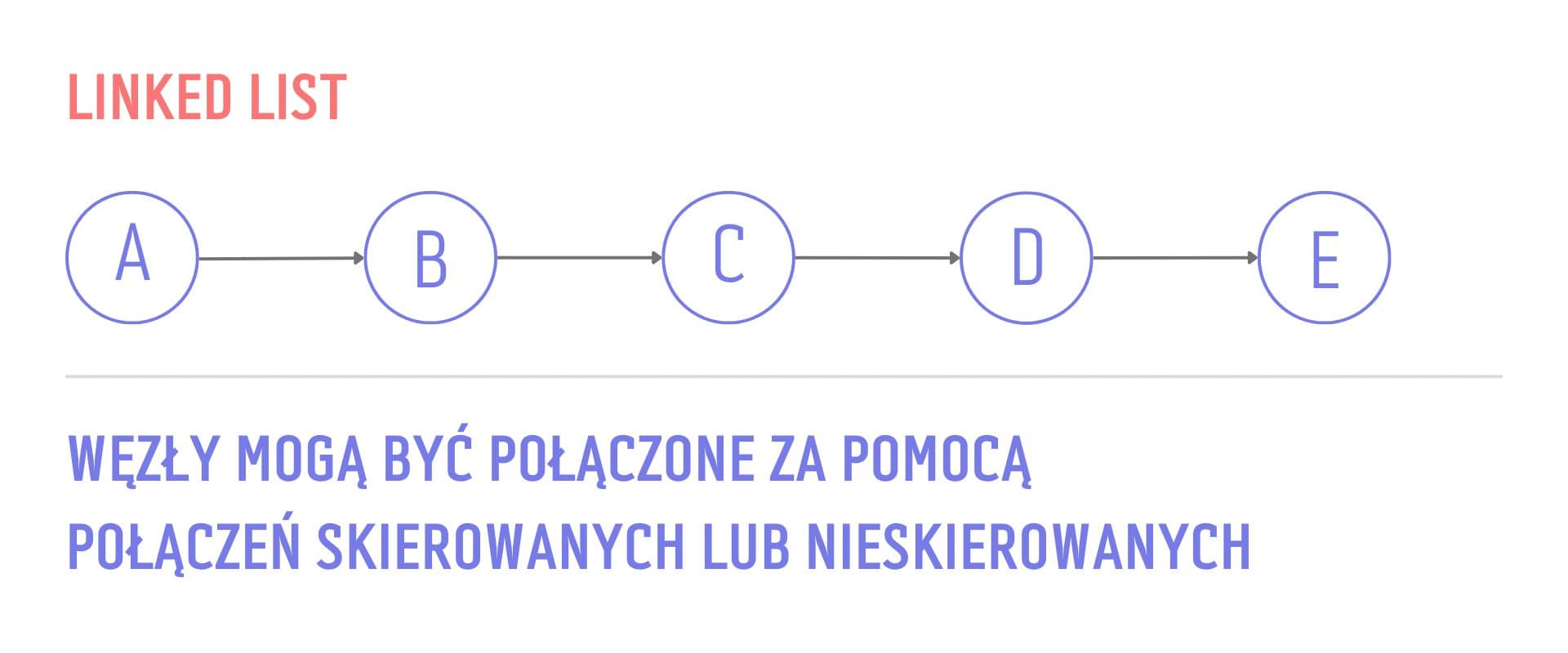
Lista połączona to jedna z najczęściej wykorzystywanych struktur

Binary Tree - drzewo binarne wzięło swoją nazwę od tego, że każdy węzeł może posiadać maksymalnie dwa węzły potomne.

Jego zastosowanie jest niezwykle szerokie - od reprezentacji hierarchi danych, przez ścieżki decyzyjne, aż po algorytmy kompresyjne, takiej jak kodowanie Huffmana.

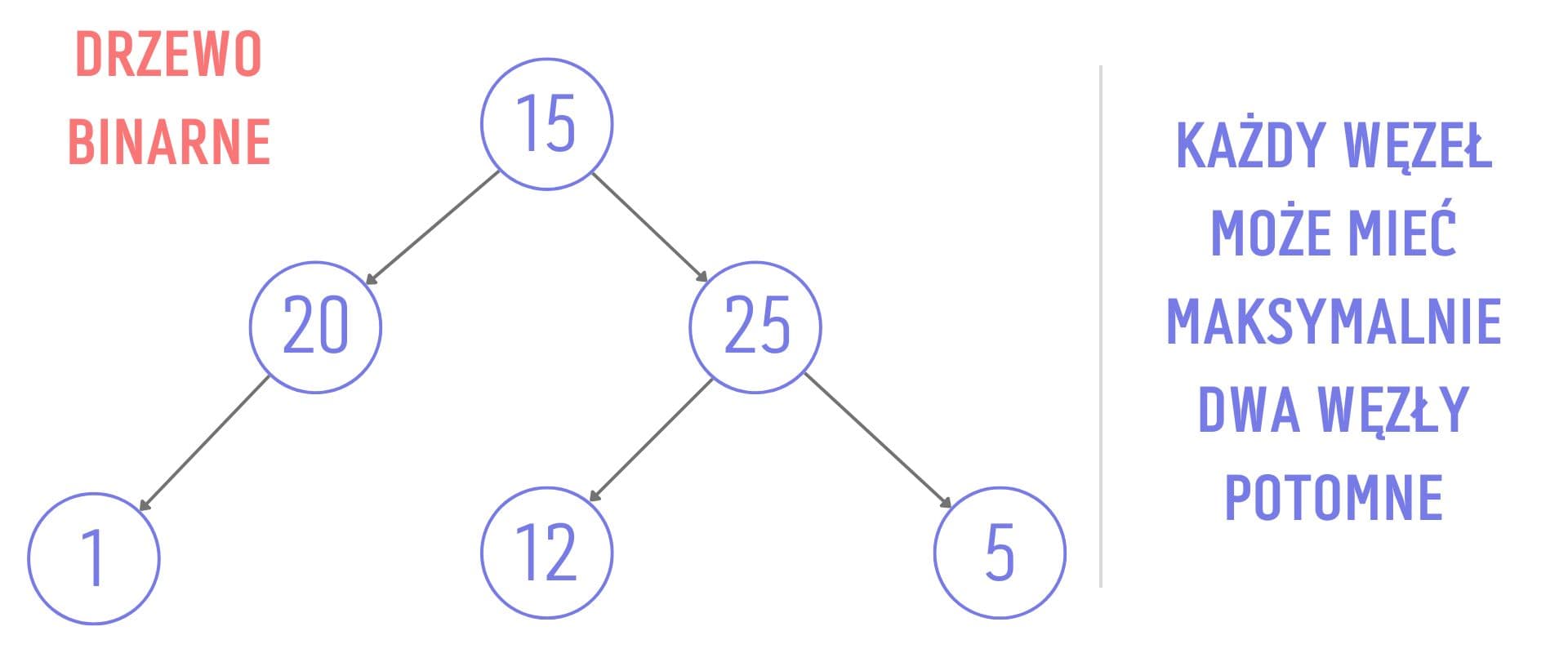
Drzewo binarne - wykorzystuje się je często w algorytmach decyzyjnych

Binary Search Tree - ta struktura jest bardzo podobna do drzewa binarnego, omówionego wyżej - każdy jej węzeł może posiadać maksymalnie dwójkę dzieci. To jednak nie koniec reguł. Węzeł znajdujący się po lewej może przechowywać tylko wartości mniejsze od rodzica, natomiast węzeł po prawej, tylko wartości większe od rodzica. Ta zasada ma zastosowanie nie tylko w relacji rodzic - dziecko, ale także w przypadku pozostałych relacji, a zatem liść znajdujący się po lewej stronie nie może mieć wartości większej od korzenia drzewa (nawet jeśli po drodze do niego znadujde się kilka innych węzłów).

Taka struktura umożliwia znalezienie konkretnego elementu w czasie logarytmicznym i najczęściej stosuje się ją do przechowywania danych, które regularnie przeszukujemy.

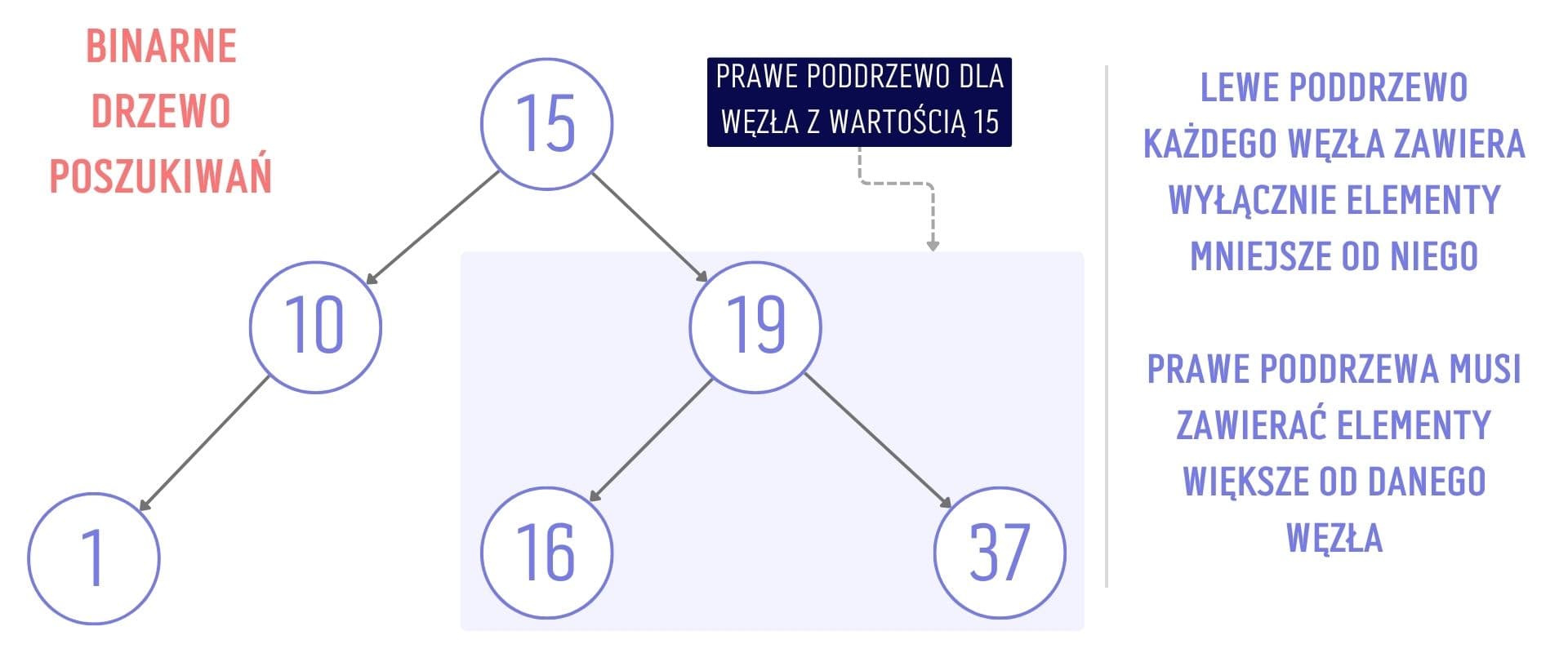
Binarne drzewo poszukiwań znajduje zastosowanie między innymi w bazach danych

Trie - drzewo nastawione na przechowywanie ciągów tekstowych i dokonywanie na nich dynamicznych operacji. Każdy węzeł przechowuje maksymalnie jedną literę i może posiadać dowolną liczbę węzłów potomnych (najczęściej jest to liczba odpowiadająca liczbie liter w alfabecie danego kraju). Liśćmi tego drzewa są frazy lub kompletne słowa, które użytkownik może chcieć wpisać (bazując na danej ścieżce w drzewie).

Ten rodzaj drzewa najczęściej wykorzystuje się do implementacji automatyczne uzupełniania tekstu - gdy użytkownik wpisuje litery (np. w pole wyszukiwania na stronie), algorytm przechodzi przez kolejne węzły w drzewie i sprawdza, jakie słowo znajduje się na końcu danej ścieżki.

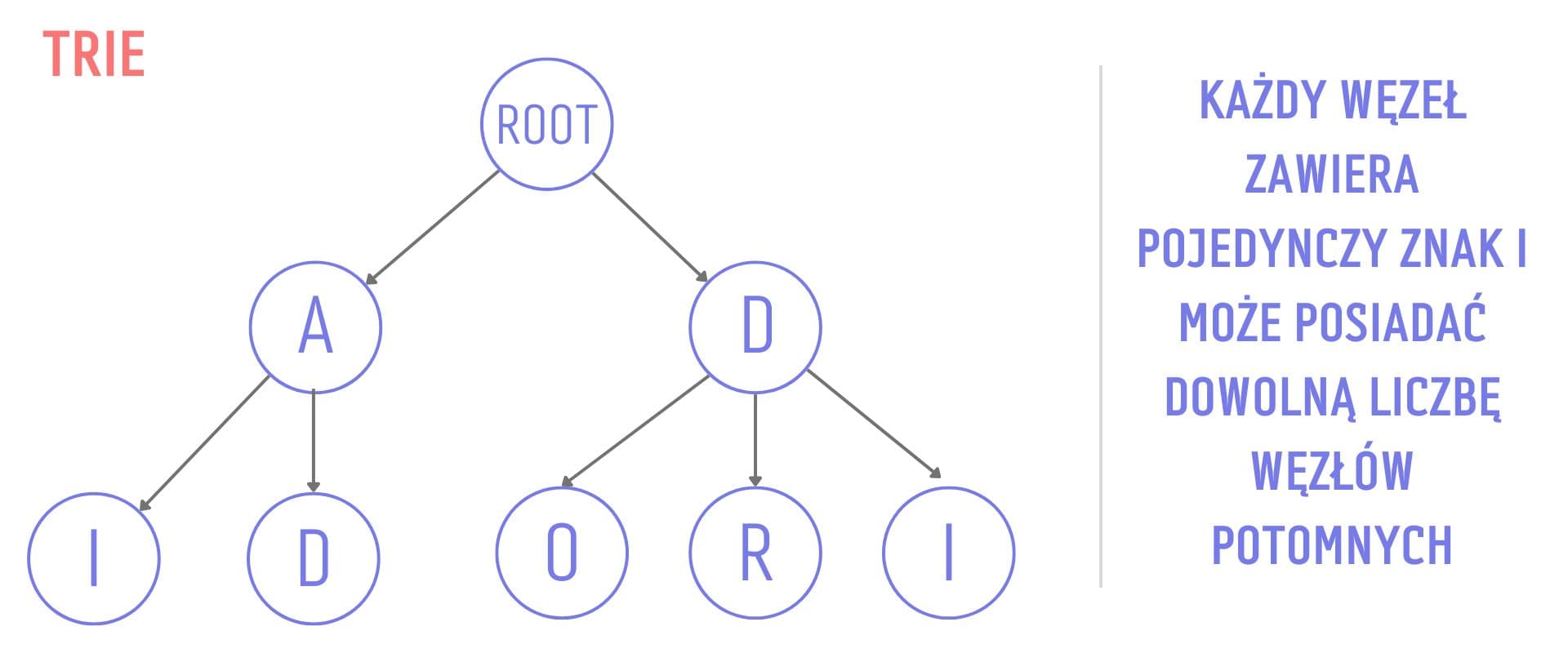
Trie - wyspecjalizowany rodzaj drzewa. Znjaduje zastosowanie m.in. w wyszukiwarkach

Każde z tych drzew powinno mieć również zaimplementowane odpowiednie metody, które umożliwą nam pracę z nim. Przykładem mogą tu być funkcje odpowiedzialne na przykład za dodawanie nowych węzłów, usuwanie istniejących lub przeszukiwanie drzewa. Wszystkie te operacje są zazwyczaj skomplikowane, a dodanie lub usunięcie węzłą wymaga nierzadko przesunięcia kilku innych węzłów w celu zachowania struktury i balansu drzewa. Jednak poznanie szczegółów implementacji każdego z nich nie jest celem tego artykułu, dlatego skupimy się jedynie na dwóch rodzajach algorytmu, który jest wykorzystywany niezwykle często podczas pracy ze strukturami drzewiastymi.

Żeby wykorzystać potencjał drzew w pełni, musimy jeszcze poznać dwa najczęściej wykorzystywane algorytmy. Mowa tu o BFS (ang. Breadth First Search) oraz DFS (ang. Depth First Search), czyli odpowiednio przeszukiwaniu drzewa najpierw wszerz oraz przeszukiwaniu najpierw w głąb.

Zacznijmy od tego pierwszego. BFS eksploruje graf wszerz, co oznacza, że zanim zejdzie głębiej, sprawdza wszystkie sąsiednie węzły na tym samym poziomie. Dzięki tej właściwości, idealnie nadaje się do znajdowania najkrótszej drogi w labiryntach reprezentowanych za pomocą grafów. Jeśli istnieje droga, to BFS znajdzie tę, która wymaga przejścia przez najmniejszą liczbę węzłów (krawędzi).

Wyobraź sobie, że masz przed sobą mapę labiryntu, na której skrzyżowanie lub ślepy zaułek to węzeł, a korytarze to krawędzie. Chcesz znaleźć najkrótszą drogę od wejścia (korzenia) do wyjścia.

Jak działa BFS?

1. Zaczynamy od wejścia, którym jest węzeł główny (korzeń).

2. Najpierw sprawdzamy wszystkie bezpośrednio dostępne korytarze (dzieci pierwszego poziomu).

3. Następnie wszystkie korytarze dostępne z tych pierwszych (dzieci drugiego poziomu) i tak dalej.

4. Ponieważ BFS przeszukuje poziom po poziomie, pierwszy raz, gdy dotrze do węzła docelowego, ma pewność, że znalazł ścieżkę z najmniejszą liczbą kroków (korytarzy).

Wbrew pozorom przeszukiwanie wirtualnych labiryntów to niezwykle popularna czynność, a jej przykładami mogą być między innymi:

• Sieci społecznościowe: Znajdowanie wszystkich znajomych drugiego stopnia (znajomych znajomych). Zaczynasz od siebie (korzeń), BFS najpierw znajduje Twoich bezpośrednich znajomych (poziom 1), a następnie znajomych Twoich znajomych (poziom 2).

• Indeksowanie stron internetowych (Web Crawling): Prosty web crawler może zaczynać od strony głównej (korzeń) i odwiedzać wszystkie linki na tej stronie (poziom 1), następnie wszystkie linki na stronach z poziomu 1 (poziom 2) itd., do pewnej głębokości.

Przeszukiwanie w głąb opiera się na podobnej zasadzie, co przeszukiwanie wszerz - również odwiedza każdy węzeł drzewa ale robi to w innej kolejności. Zamiast sprawdzać wszystkie węzły na danym poziomie, od razu stara się dotrzeć jak najgłębiej. Następnie powtarza tą czynność dla wszystkich pozostałych węzłów na danym poziomie.

DFS sprawdza się idealnie w rozwiązywaniu problemów, gdzie trzeba zbadać jedną pełną ścieżkę do końca, zanim spróbuje się innej. Jest również bardziej oszczędny pamięciowo niż BFS w przypadku bardzo szerokich drzew, ponieważ przechowuje tylko bieżącą ścieżkę.

Algorytm ten najczęściej stosuje się do:

• Sprawdzania cykli w grafie: DFS może być użyty do wykrycia, czy w grafie (lub drzewie, jeśli jest niepoprawnie połączone) istnieje cykl. Jeśli podczas eksploracji DFS natrafi na już odwiedzony węzeł, który jest częścią bieżącej ścieżki, oznacza to cykl.

• Generowanie wszystkich możliwych kombinacji/permutacji: Na przykład, aby wygenerować wszystkie możliwe sposoby ułożenia zestawu klocków, DFS może eksplorować każdą sekwencję umieszczania klocków.

• Sortowanie topologiczne: Uporządkowanie zadań, które mają zależności (np. "zadanie A musi być wykonane przed zadaniem B"). DFS pomaga ustalić prawidłową kolejność

Do tej pory poruszyliśmy teorię oraz podstawowe algorytmy. Teraz przyszedł czas na zastanowienie się, gdzie możemy wykorzystać te umiejętności w praktyce. Przy omawianiu grafów pokazałem również przykład porównujący graf do mapy. To porównanie nie było oczywiście przypadkowe, a mapy i systemy nawigacji są jednym z miejsc, w których bardzo często wykorzystuje się te struktury.

W świecie frontendu istnieje jeszcze wiele innych zastosowań dla drzew, a najpopularniejsze z nich to:

• Menu Drzewiaste - wiele stron posiada rozbudowaną strukturę menu, którą można przedstawić w kodzie za pomocą drzewa. Przykład takiego menu znajdziesz choćby na Allegro. Po kliknięciu w “Kategorie” zobaczysz wiele dostępnych opcji. Oznacza to, że “Kategorie” to węzeł główny od którego wychodzą kolejne węzły potomne: Elektronika, Moda, Dom i ogród, itd.. Te z kolei dzielą się na kolejne węzły - w przypadku elektroniki są to: AGD, Komputery itd.. Po kolejnym podziale dochodzimy do końca drzewa, a więc do węzłów liści (np. Laptopy).

• Efektywne Przeszukiwanie - struktury drzewiaste są często stosowane do szybkiego przeszukiwania i wyciągania potrzebnych danych. Zastosowanie drzewa binarnego (lub jego odmiany, na przykład: AVL tree lub Red-black tree) może znacząco przyspieszyć znalezienie potrzebnych informacji. Jest to szczególnie przydatne w przypadku dużych zbiorów danych.

• Tablice Mieszające - drzewa znajdują zastosowanie także w tablicach mieszających. Przydają się do obsługi kolizji w przypadku wystąpienie dwóch identycznych hashy. Więcej na temat tablic mieszających dowiesz się w tym artykule.

• DOM - Document Object Model również opiera się na strukturze drzewa, a programiści frontend często korzystają z tego faktu nieświadomie, korzystając z metod do wyszukiwania elementów i modyfikacji struktury HTML.

• Biblioteki - wiele bibliotek, zarówno frontendowych jak i backendowych, wykorzystuje struktury drzewiaste do przechowywania informacji oraz stanu aplikacji. Twórcy frameworków (np. React) także wykorzystują drzewa. Najczęściej przechowując w nich dane wprowadzone przez użytkownika lub wewnętrzny stan biblioteki (np. wirtualny DOM).

Oczywiście drzewa nie są stosowanie tylko we frontendzie. Prawdę mówiąc, zdecydowana większość ich zastosowań ma miejsce właśnie w innych dziedzinach. Najczęściej spotkamy je w bazach danych, matematyce, biologii i sztucznej inteligencji. Jeśli jednak poszukamy dokładnie, to okaże się, że drzewa używane są w niemal każdej dziedzinie życia i każdy z nas korzysta z nich codziennie za pośrednictwem używanych aplikacji.

Drzewa są wszechobecne. Mimo, że na co dzień nie zauważamy ich obecności, to w praktyce znajdziemy je w niemal każdej aplikacji pod różną postacią. Właśnie dlatego, jako programiści, powinniśmy znać ich podstawowe rodzaje, zastosowanie oraz możliwości. 

Nie chodzi tu jednak o znajomość każdego możliwego drzewa, algorytmu, czy też terminu związanego z tym tematem. Wystarczy ogólna wiedza na ich temat i odrobina praktyki w wykorzystaniu, żeby zacząć dostrzegać możliwe zastosowania w codziennej pracy. Jeżeli nie mamy pojęcia o istnieniu danego zagadnienia, to nie możemy też wiedzieć, kiedy zastosować je w praktyce, a w najgorszym przypadku może się okazać, że wynajdujemy koło od nowa, na dodatek w gorszej, mniej sprawdzonej w boju, wersji.

W artykule poruszyłem jedynie podstawowe pojęcia, rodzaje drzew i algorytmy wykorzystywane do pracy z drzewami i grafami. Jeżeli jesteś zainteresowany/a dalszym zgłębianiem tego tematu, to solidne podstawy, wyjaśnione w przystępny sposób, (dotyczące nie tylko drzew ale również wielu innych struktur danych) możesz znaleźć w tej książce.